束（Lattice）の話

　二つの定義は同値である． 実際，先のように半順序$\le$によって定義された束において$\{x,\ y\}$の下限と上限とを$x\wedge y$と$x\vee y$とで表せば，これらは上の法則に従う． 逆に，この法則に従う二項演算$x\wedge y,\ x\vee y$の定義された集合$L$において，$y\wedge x = x$であることを（あるいは$x\vee y = y$であることを）$x\le y$で表わせば，関係$\le$は$L$の順序であり，$L$の任意の2元$x,\ y$に対し，$x\wedge y$と$x\vee y$とは，この順序に関する$\{x,\ y\}$の下限と上限となる．
例
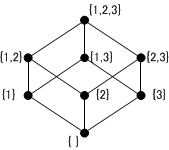
  1. 任意の集合$S$に対して，そのべき集合$\mathcal{P}(S)$を集合の包含関係によって順序集合とみなすと，$A,\ B\in\mathcal{P}(S)$に対し，$A\cap B$と$A\cup B$とが$\{A,\ B\}$の下限と上限となるので，この順序集合は束となる．
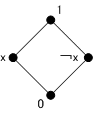
  2. 上の例で特に$S$として唯一つの元からなる集合をとれば，$\mathcal{P}(S)$は$S$自身と空集合$\phi$とから成る．これらを$1$と$0$とで表し$\cap$と$\cup$とを$\wedge$と$\vee$とに書き換えれば，$1\wedge 1=1,\ 1\wedge 0=0\wedge 1=0\wedge 0=0,\ 1\vee 1=1\vee 0=0\vee 1=1,\ 0\vee 0=0$が成り立つ． 従って逆に，集合$T=\{1,\ 0\}$上の二項演算$\wedge$と$\vee$をこれらの式によって定義すれば，$T$は束である

分配束（distributive lattice）

　次の二法則に従う束を分配束という．
  1. 分配律1：$(x\vee y)\wedge z=(x\wedge z)\vee(y\wedge z)$
  2. 分配律2：$(x\wedge y)\vee z=(x\vee z)\wedge(y\vee z)$
先に挙げた例はいずれも分配束である．

ブール束（Boolean lattice）

　最大元$1$と最小元$0$とをもつ分配束において，さらに各元$x$に対して$x\wedge\lnot x=0,\ x\vee\lnot x=1$をみたす元$\lnot x$が存在するとき，この束はブール束（ブール代数：Boolean algebra）であるといい，$\lnot x$を$x$の補元とよぶ． 補元は唯一つに定まる．
　先に挙げた例の$\mathcal{P}(S)$と$T$とはブール束である．
　　
演算命題論理ブール代数備考
論理積$\land$$\cdot$$\cdot$は省略可能
論理和$\lor$$+$　
否定$\lnot$$\overline{　}$　

ブール代数の公理

交換法則　$A+B=B+A$　$A\cdot B=B\cdot A$
分配法則　$A\cdot(B+C)=A\cdot B+A\cdot C$　$A+(B\cdot C)=(A+B)\cdot(A+C)$
単位元　$A+0=A$　$A\cdot 1=A$
補元　$A+\overline{A}=1$　$A\cdot\overline{A}=0$

ブール代数の定理（双対の原理）

　ブール代数では，元の式の$+$と$\cdot$，$0$と$1$を交換してできる式を，元の式の「双対」(dual)と呼ぶ． ブール代数において，ある定理が成り立つならば，その定理の双対もまた成り立つ．

ブール代数の定理

結合律　$A+(B+C)=(A+B)+C$　$A\cdot(B\cdot C)=(A\cdot B)\cdot C$
吸収律　$A+(A\cdot B)=A$　$A\cdot(A+B)=A$
巾等律　$A+A=A$　$A\cdot A=A$
　$A+1=1$　$A\cdot 0=0$
ド・モルガン　$\overline{A+B}=\overline{A}\cdot\overline{B}$　$\overline{A\cdot B}=\overline{A}+\overline{B}$
二重否定　$\overline{\overline{A}}=A$
戻る