- 反射律: 任意の元$a$について$a\le a$
- 推移律: $a\le b$かつ$b\le c$ならば$a\le c$ ←要するに、三竦みが無いってこと!
- 反対称律: $a\le b$かつ$b\le a$ならば$a=b$
- 完全律: $A$の任意の元$a,\ b$について$a\le b$か$b\le a$のどちらかが成り立つ
ハッセ線図(Hasse diagram)
順序集合$(A,\le)$は、
- $A$の各要素に対し、$xy$座標の定められた平面上に点$P_a$をとる。
- $A$の異なる要素には平面上の異なる点をとるものとする。
- $a\le b$ならば、$P_a$の$y$座標より$P_b$の$y$座標を大きくなるようにしておく。
- $a\le b$であり、$a\le c$かつ$c\le b$なる$c\in A$が存在しないとき、$P_a$と$P_b$を線分で結ぶ。
例
$S=\{1,\ 2,\ 3,\ 4,\ 5,\ 6\}$、
$m|n$を「$m$が$n$の約数である」という関係であるとするとき、
$(S,\ |)$は半順序集合となり、以下の様にハッセ線図で表すことができる。
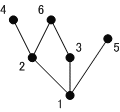
$(S,\ |)$は半順序集合となり、以下の様にハッセ線図で表すことができる。

上限、下限、その他
順序集合の空でない部分集合$A$について...
|
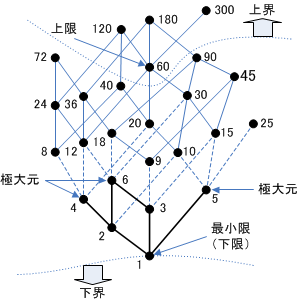
|
- 上限(最小上界)(least upper bound, supremum)
上界の最小元のこと。$\sup(A)$と書く。
- 下限(最大下界)(greatest lower bound, infimum)
下界の最大元のこと。$\inf(A)$と書く。