整列２分木：ヒープ（heap）

• 整列２分木（heap）とは、以下の条件を満たすラベル付き木である：
  1. 完全２分木である。 但し最下段（レベル０）だけは例外で、左から順に詰まっていれば、頂点（ノード）が存在しなくても良い。 レベル１の頂点の内、子が１個のものは高々１個で、あれば左の子だけを持つ。
     
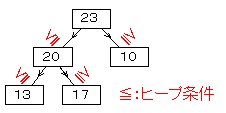
  2. 各頂点が「頂点のラベルは何れの子のラベルよりも小さくない」というヒープ条件（heap condition）を満たしている。
  

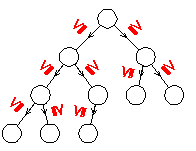
ヒープ（heap）に対する操作

　挿入（Insert）

1. 新たなノードをヒープの最後に追加する
2. そこから上（ルート）に向かって所定の位置まで移動する(⇒図)
   ↑この操作をふるい上げ（sift-up）と呼ぶ

　ルートの削除（Delete）

1. ルートのノードを削除する
2. ヒープの最後のノードをルートに移動する
3. そこから下（リーフ）に向かって所定の位置まで移動する(⇒図)
   ↑この操作をふるい下げ（sift-down）と呼ぶ

　削除（Delete）

1. 指定されたノードを削除する（それがヒープの最後のノードだったなら、これで終り）
2. ヒープの最後のノードをそこに移動する
3. 削除したノードより大きい（or小さい）場合は、ふるい上げ（orふるい下げ）を行う
   

整列２分木：ヒープ（heap）の配列を使った実現

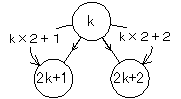
• このように頂点に通し番号を付けると、頂点ｋの左右の子の番号はそれぞれ２ｋ、２ｋ＋１で表され、頂点ｎの親の番号はｎ／２（切捨）で表される
  
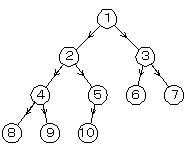
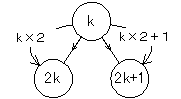
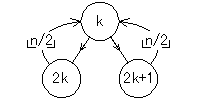
• 頂点の番号をインデックスとみなして、ラベルデータを配列に格納することができる（Ｃの配列のインデックスとは異なり１から始まるものとする→Ｃ版）
  

整列２分木：ヒープ（heap）の配列を使った実現（in Ｃ）

• このように頂点に通し番号を付けると、頂点ｋの左右の子の番号はそれぞれ２ｋ＋１、２ｋ＋２で表され、頂点ｎの親の番号は（ｎ−１）／２（切捨）で表される
  
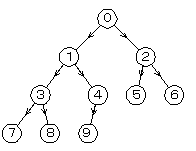
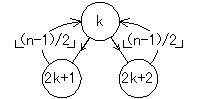
• 頂点の番号をインデックスとみなして、ラベルデータを配列に格納することができる