グラフ（graph）の話

• グラフ（graph）$G=(V,E)$は， 頂点（vertex）の空でない有限集合$V$と辺（edge）の集合$E$からなる．
• 頂点は点，節点（node）とも呼ばれる， 辺は枝（branch, arc）とも呼ばれる．
• 辺が頂点の順序対$(v,w)$で与えられる場合， そのグラフを有向（directed）グラフという．
• $v$は辺$(v,w)$の始点（tail），$w$は辺の終点（head）と呼ばれる．
• 辺が相異なる頂点の非順序対$(v,w)$で与えられる場合， そのグラフを無向（undirected）グラフという．

• $(v,w)\in E$のとき， 頂点$w$は頂点$v$に隣接（adjacent）するという． また，$(v,w)$を$v$から$w$への辺ともいう．
• $v$に隣接する頂点の個数を$v$の出次数（out degree）， $w$が隣接する頂点の個数を$w$の入次数（in degree）という．
• 無向グラフの場合の頂点の次数（degree）は，それに隣接する頂点の個数である．

• 有向道（directed path）とは，$(v_1,v_2),\ (v_2,v_3),\dots,\ (v_{n-1},v_n)$という辺の列である．
  これを$v_1$から$v_n$への有向道といい，その長さは$n-1$である．
• $v$から$w$への有向道が存在するとき，$w$は$v$から到達可能（reachable）であるという．
• 全ての頂点がある頂点$r$から到達可能であるとき，この$r$を根（root）という．
• 道はその辺が全て異なるとき単純（simple）であるという．
• 道はその頂点が全て異なるとき初等的（elementary）であるという． 但し最初と最後の頂点は一致しても良い．
• 閉路（circuit, loop, closed path）とは，同じ頂点で始まりかつ終わる，長さ$1$以上の道のことである．
• 有向閉路，サイクル（cycle）とは，同じ頂点で始まりかつ終わる，長さ$1$以上の有向道のことである．

グラフの表現方法

　辺行列（edge matrix）

• 行$(i,j)$が辺$(v_i,v_j)$を表しているように，各行が$G$の辺を意味している$m\times2$の整数行列

　接続行列（incident matrix）

• 頂点$v_j$に辺$e_i$が接続している時$m_{ij}=1$，接続していない時$m_{ij}=0$とした$n\times m$の行列
  （有向グラフの場合は，頂点$v_j$から$v_k$への有向枝$e_i$が有る時$m_{ji}=-1,\ m_{ki}=+1$）

　隣接行列（adjacency matrix）

• 頂点$v_i$から$v_j$への有向枝が有る時$a_{ij}=1$，無い時$a_{ij}=0$とした$n\times n$の正方行列
  （無向グラフの場合は有向枝が双方向に接続していると見なせば良い） $$A=\left(\begin{array}{c} a_{11} & a_{12} & \cdots & a_{1n}\\ a_{21} & a_{22} & \cdots & a_{2n}\\ \vdots & \vdots & \ddots & \vdots\\ a_{n1} & a_{n2} & \cdots & a_{nn}\\ \end{array}\right)$$

　隣接点リスト（adjacency list）

• 一般に枝の個数は$n\times n$に比べて極めて小さく，隣接行列の要素は殆どが$0$となるので， 各頂点$v_i$に隣接している頂点をリストとして管理した方が効率が良い

　例

	$B=\left(\begin{array}{c} 1 & 2\\ 1 & 3\\ 3 & 2\\ 4 & 3\\ 4 & 5\\ 5 & 4\\ \end{array}\right)$	$M=\left(\begin{array}{c} -1 & -1 & 0 & 0 & 0 & 0\\ +1 & 0 & +1 & 0 & 0 & 0\\ 0 & +1 & -1 & +1 & 0 & 0\\ 0 & 0 & 0 & -1 & -1 & +1\\ 0 & 0 & 0 & 0 & +1 & -1\\ 0 & 0 & 0 & 0 & 0 & 0\\ \end{array}\right)$
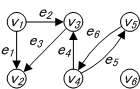
グラフ	辺行列	接続行列
$A=\left(\begin{array}{c} 0 & 1 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0\\ \end{array}\right)$
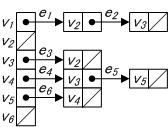
隣接行列	隣接点リスト

有向木（directed tree）^{cf 無向木へ}

• 有向木（directed tree）とは，閉路のない有向グラフ（directed acyclic graph）で，以下の条件を満たす：
  1. 根（root）と呼ばれる，入次数（in deegree）が$0$の頂点が存在する
  2. 根以外の頂点の入次数（in degree）は$1$である
  3. 各頂点には，根からそれに至る有向道が存在する
• 根付木（rooted tree）とも呼ばれる．

• $F=(V,E)$を木とする．$(v,w)\in E$のとき，$v$は$w$の親（father）といい，$w$は$v$の子（son）といわれる．
• $v$から$w$への有向道が存在するとき，$v$は$w$の先祖（ancester）といい，$w$は$v$の子孫（descendant）といわれる．
• 子を持たない頂点は，葉（leaf）と呼ばれる．
• 頂点$v$とその子孫全体は$F$の部分木（subtree）といわれる． 頂点$v$はその部分木の根である．
  

• 木の頂点$v$の深さ（depth），レベル（level）とは，根から$v$への有向道の長さである．
• 木の頂点$v$の高さ（height）とは，$v$から最も遠い葉への有向道の長さである．
• 木の高さ（height）とは，その根の高さである．

• 順序木（ordered tree）とは，各頂点の子の間に順序が付いている木のことである．
• 順序木を描くときは，各頂点の子は左から右へ順番に書くものとする．

２分木（binary tree）

• ２分木（binary tree）とは，以下のような順序木である：
  1. 各頂点の子は左の子（left son）または右の子（right son）として区別されている
  2. どの頂点の左の子も右の子も高々$1$個である
• 根が頂点 $v$の左の子である部分木$T_l$を$v$の左部分木（left subtree）， 同様に，その根が頂点$v$の右の子である部分木$T_r$を$v$の右部分木（right subtree）という．
• 以下のような２分木を完全（complete）２分木という：
  ある整数$k$が存在して，

  1. 深さ$k$未満の頂点が全て左右の子を持つ
  2. 深さ$k$の頂点が全て葉である
• 高さ$k$の完全２分木は$2^{k+2}-1$個の頂点を持つ

木の走査（traverse）

　先行順走査（preorder traverse）

• 行きがけ順とも呼ばれる．
• $T$の先行順走査（preorder traverse）は以下の様に帰納的に定義される：
  1. 根$r$を訪問（走査）する
  2. 根$v_1,\ v_2,\dots,\ v_k$を持つ部分木をこの順に先行順で訪問する．

　後行順走査（postorder traverse）

• 帰りがけ順とも呼ばれる．
• $T$の後行順走査（postorder traverse）は以下の様に帰納的に定義される：
  1. 根$v_1,\ v_2,\dots,\ v_k$を持つ部分木をこの順に後行順で訪問する．
  2. 根$r$を訪問する

　中間順走査（inorder traverse）

• 中がけ順とも呼ばれる．
• ２分木$T$に対する中間順走査（inorder traverse）は以下の様に帰納的に定義される：
  1. 根$r$の左部分木を（もし在れば）中間順で訪問する．
  2. 根$r$を訪問する
  3. 根$r$の右部分木を（もし在れば）中間順で訪問する．

無向木（undirected tree）^{cf 有向木へ}

• 無向木（undirected tree）とは，閉路のない無向グラフで，連結（connected：任意の２頂点間に道がある）なものをいう．
• 根付き（rooted）無向木とは，特定の頂点が根として指定されている無向木をいう．

• 有向木の全ての辺の向きを無くすと無向木になる
• 根付き無向木に対しても，有向木と同様な述語を用いる
• 違いは：

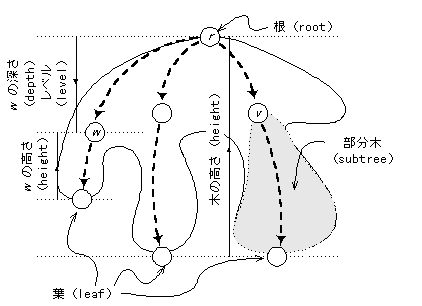
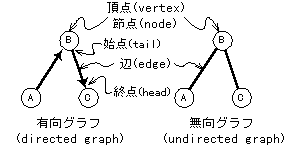
  有向木	全ての有向道が先祖から子孫へ行く
  無向木	両方向の道が存在する

ラベル付きグラフ（labeled graph）

• ラベル付きグラフ（labeled graph）とは，各頂点$v$にラベルが与えられているグラフである．

重み付きグラフ（weighted graph）

• 重み付きグラフ（weighted graph）とは，各辺$k=(u,v)$に重み$w(k)=w(u,v)$が与えられているグラフである．