演算子（operator）

演算子

　２項算術演算子

演算子	機能		備考
+	加算	足し算	a + b	a がポインタの時は特別
-	減算	引き算	a - b	a がポインタの時は特別
*	乗算	掛け算	a * b
/	除算	割り算	a / b	整数型同士で被演算数が負の場合の切り捨て方向は処理系依存	`a == (a/b)*b + a%b` は保証される
%	剰余	割り算の余り	a % b	整数型同士で被演算数が負の場合の結果の符合は処理系依存	`a == (a/b)*b + a%b` は保証される

　ポインタの加減算

演算のパターン	結果の値と型
ポインタ型 + 整数型	その数だけ後ろ要素を指すポインタ
ポインタ型 - 整数型	その数だけ前の要素を指すポインタ
ポインタ型 - ポインタ型	ポインタに挟まれた要素数を表す整数

その他の演算と型に関してはこっち

　単項算術演算子

演算子	機能	備考
+	プラス	+a
-	マイナス	-a

　ビット毎の論理演算子

演算子	機能	備考
&	ビット毎の論理積	a & b	ビットマスクに使われる
\|	ビット毎の論理和	a \| b	ビットオンに使われる
^	ビット毎の排他的論理和	a ^ b	ビット反転に使われる
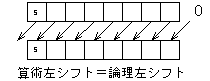
<<	左シフト	a << b	aをbビット左シフト（右から0が入る） 2^bを掛けるのと同じ
>>	右シフト	a >> b	aをbビット右シフト符号無し数の場合：　論理シフトで、2^bで割るのと同じ符号付き数の場合：　論理シフト／算術シフトは処理系依存
~	１の補数	~a	aの各ビットの0／1を反転する

（<と<や >と>の間に空白（スペース）を入れてはいけない！）

各ビット演算の結果
被演算ビット		論理積（AND）	論理和（OR）	排他的論理和（XOR）	論理否定（NOT）
`a`	`b`	`a & b`	`a \| b`	`a ^ b`	`~a`
0	0	0	0	0	1
0	1	0	1	1	1
1	0	0	1	1	0
1	1	1	1	0	0

１ビットシフトの結果


符号ビット（ｓ）が保存される　→

　代入演算子

式₁ = 式₂

式₂の値を式₁の型に変換して代入
代入式の型は左辺（式₁）の型で、値は代入後の値
式₁は左辺値でなければならない
左辺値とは
- 変更可能
- 配列や関数は駄目
- const修飾禁止

式₁ op= 式₂

２項演算子（op）と代入演算子「=」が合体したもので、
式₁が一度だけ計算されることを除いて、式₁ = (式₁) op (式₂)と同じ
+=, -=, *=, /=, %=, <<=, >>=, &=, |=, ^= がある
（演算子を構成している記号の間に空白（スペース）を入れてはいけない！）

　インクリメント・デクリメント演算子

演算子	前置（++a, --a）	後置（a++, a--）
++	aの値を使用する前に、インクリメント（１増やす）	aの値を使用した後に、インクリメント（１増やす）
--	aの値を使用する前に、デクリメント（１減らす）	aの値を使用した後に、デクリメント（１減らす）

（+と+や -と-の間に空白（スペース）を入れてはいけない！）

式の中に++や--が含まれている場合の考え方

++iを１個含む式	⇒	++i; 式中の++iをiに置き換えた式
例：　j = ++i;	⇒	++i; j = i;
i++を１個含む式	⇒	式中のi++をiに置き換えた式 i++;
例：　j = i++;	⇒	j = i; i++;

変数（k）の値を１増やす方法
1. k = k + 1;
2. k += 1;
3. ++k;
4. k++;
ポインタ型の場合は、前（--）後（++）の要素を指すようになる

　関係演算子

演算子	機能	数学	備考
>	より大きい	＞	算術演算子よりも優先順位が低く論理演算子よりも優先順位が高い結果はint型で、真のとき１、偽のとき０
>=	以上	≧
<	より小さい	＜
<=	以下	≦
== ^※	等しい	＝
!=	等しくない	≠

^※ 代入演算子 = と間違わないように！
（演算子を構成している記号の間に空白（スペース）を入れてはいけない！例： > = はＮＧ！）

真理値としては、ノンゼロ（０でない）が真で、ゼロ（０）が偽と解釈される

　論理演算子

演算子	機能	備考
&&	論理積（AND）	式₁ && 式₂	式₁の値が０（偽）のとき　式₂を実行せずに、０（偽）式₁の値が０でない（真）のとき　式₂を実行して、　　その値が０（偽）ならば０、　　０でない（真）ならば１	結果はint型で、真のとき１、偽のとき０
\|\|	論理和（OR）	式₁ \|\| 式₂	式₁の値が０でない（真）のとき　式₂を実行せずに、１（真）式₁の値が０（偽）のとき　式₂を実行して、　　その値が０（偽）ならば０、　　０でない（真）ならば１
!	論理否定（NOT）	!式₁	式₁が０でない（真）のとき０式₁が０（偽）のとき１

（演算子を構成している記号の間に空白（スペース）を入れてはいけない！例： & & はＮＧ！）

結果の論理値
被演算式		論理積（AND）	論理和（OR）	論理否定（NOT）
`式₁`	`式₂`	`式₁ && 式₂`	`式₁ \|\| 式₂`	`!式₁`
偽	偽	偽	偽	真
偽	真	偽	真	真
真	偽	偽	真	偽
真	真	真	真	偽

真理値としては、ノンゼロ（０でない）が真で、ゼロ（０）が偽と解釈される

　条件式

( 式_条件 ) ? 式_T : 式_F

式_条件が、０でない（真）ならば式_Tが実行され、０（偽）ならば式_Fが実行される
一般に式_条件の括弧()は不要だか分かりやすさのために付けておく方が良い
制御の流れとしては、
if( 式_条件 )
式_T;
else
式_F;

と同じだが、条件式は文ではなく式である
最終的な式の値は、式_条件、の真偽に応じて、式_T または式_F の値となる
MS-ExcelのIF関数：IF(論理式,真の場合,偽の場合) に似ている

　sizeof

sizeof オブジェクト
sizeof( 型名 )

オブジェクトのサイズ（バイト数）に等しい整数
コンパイル時にオブジェクトサイズの計算ができる

　コンマ

式₁ , 式₂

式₁式₂の順に実行される
コンマ式の値と型は式₂に一致する
これでfor文の各部分等、式を一個しか書くことがない場所、に多くの式を置くことができる

　キャスト（cast）

(型名)式

明示的に型変換するときに用いる

演算子の優先順位と結合規則

優先順位	演算子	結合規則	備考
高 ↑ ↓ 低	`()`　`[]`　`->`　`.`	→	関数、配列、構造体
	`!`　`~`　`++`　`--`　`+`　`-`　`*`　`&`　`(型)`　`sizeof`	←	単項
	`*`　`/`　`%`	→	２項（乗、除、剰余）
	`+`　`-`	→	２項（加、減）
	`<<`　`>>`	→	ビットシフト（左、右）
	`<`　`<=`　`>`　`>=`	→	比較
	`==`　`!=`	→	比較
	`&`	→	ビット毎の論理積
	`^`	→	ビット毎の排他的論理和
	`\|`	→	ビット毎の論理和
	`&&`	→	論理積
	`\|\|`	→	論理和
	`? :`	←	条件式（３項）
	`=`　`+=`　`-=`　`*=`　`/=`　`%=` 　`&=`　`^=`　`\|=`　`<<=`　`>>=`	←	代入
	`,`	→	コンマ

優先順位等について心配なときは明示的に括弧()で囲めば良い
変数名と演算子から作られるものが式である

　優先順位

優先順位が高い演算子から順に演算が実行される。

a + b * c ⇔ a + ( b * c )

　結合規則

同じ優先順位の演算子が並んだ時、

→：左から右へ演算が実行される。
　a / b / c ⇔ ( a / b ) / c
←：右から左へ演算が実行される。
　a = b = c ⇔ a = ( b = c )

数学との違いについて

数学	意味	Ｃの式	備考
ｘ＝１	ｘに 1 を代入する	x = 1	代入演算子、　`==` と間違わないこと
ａ＝ｂ	ａとｂが等しい	a == b	関係（比較）演算子、　`= =` ではダメ、`=` と間違わないこと
ａ ≠ ｂ	ａとｂが等しくない	a != b	関係（比較）演算子、　`! =` や `<>` ではダメ、論理否定を使って `!(a==b)` でも良い
ａ ≧ ｂ	ａはｂ以上	a >= b	関係（比較）演算子、　`> =` ではダメ
ａ ≦ ｂ	ａはｂ以下	a <= b	関係（比較）演算子、　`< =` ではダメ
ａ＝ｂ＝０	ａ、ｂに０を代入する	a = b = 0	代入演算子、　場所によっては `a = 0; b = 0;` や `a = 0, b = 0` でも良い
ａ＝ｂ＝０	ａもｂも０に等しい	a == 0 && b == 0	関係（比較）演算子と論理演算子、　`a == b == 0` はダメ
１＜ｘ＜３	ｘは１より大きく、３より小さい	1 < x && x < 3	関係（比較）演算子と論理演算子、　`1 < x < 3` はダメ
ｘ ≦ １，３ ≦ ｘ	ｘは１以下または３以上	x <= 1 \|\| 3 <= x	関係（比較）演算子と論理演算子、　`x <= 1, 3 <= x` はダメ
ａ＝２，ｂ＝４	ａは２、ｂは４に等しい	a == 2 && b == 4	関係（比較）演算子と論理演算子、　`a == 2, b == 4` はダメ

数学では等号（＝）を代入と等号の両方の意味に用いる
Ｃでは演算子に１バイト文字しか使えないので、≧ 等は >= 等になる
数学では，が、‘かつ’の意味で使われたり、‘または’の意味で使われたりするが、
Ｃでは、&& や || を用いて、論理を厳密に記述しなければならない

脚注

代入演算子（x op= y）について

#define	NUM	10
int	a[NUM], *p;

/* Ａ　　配列 a の全ての要素を 0 にする */
for( i = 0; i < NUM; i++ )
	a[i] = 0;
	
/* Ａ’　配列 a の全ての要素を 0 にする */
for( i = 0; i < NUM; )
	a[i++] = 0;	/* 後置インクリメント演算子++を用いてこのように記述できる *

/* Ｂ　　配列 a のそれぞれの要素を 3 ずつ増やす */
for( i = 0; i < NUM; i++ )
	a[i] = a[i] + 3;

/* Ｂ’　配列 a のそれぞれの要素を 3 ずつ増やす */
for( i = 0; i < NUM; i++ )
	a[i] += 3;	/* 代入演算子+=を用いてこのように記述できる */

/* Ｂ''　配列 a のそれぞれの要素を 3 ずつ増やす */
for( i = 0; i < NUM; )
	a[i++] += 3;	/* 後置インクリメント演算子++を用いてこのように記述できる */

/*
　　ここで、x op= y を機械的に x = x op y と置き換えてみると、
	a[i++] += 3;　は、
	a[i++] = a[i++] + 3;　となるが、
	これでは、i の値は 2 増えてしまうし、
　　所望の結果は得られない！
　　（実際には置き換え処理が行われているのではないってこと！）

　　x op= y は、
	p = &x;		//　値を格納すべき場所（元の x のアドレス）を求めておき
	*p = *p op y;	//　元の x の値と y の値を演算（op）し、その結果を格納すべき場所に入れる
　　と実際には動いている
　　例えば、a[i++] += 3; の場合は、
	p = &a[i++];
	*p = *p + 3;
*/

このややこしい？演算子（x op= y）の存在意義は、x = x op y という有り勝ちな演算パターンに対して、

x を１回書くだけで済ませることができる
→ x が複雑な式の場合には、簡便化が達成される
x の値を得たり、値を格納する為の場所（アドレス）の計算を１回で済ませることができる
→ x が複雑な式の場合には、効率の良い実行コード（小さくて速い！）が生成される