組合回路（論理ゲート）

  1. AND（論理積）
    ゲート： 真理値表
    $\ A\ $$\ B\ $$\ Z\ $
    000
    010
    100
    111
    論理式： $Z=AB$
    多入力になると、$Z=ABCD\cdots$　（全てが$1$の時のみ$1$）
    $Z=\overline{\overline{A}+\overline{B}+\overline{C}+\overline{D}+\cdots}$　ととらえると（何れかが$0$の時$0$）
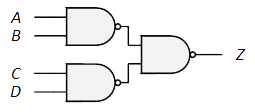
    等価回路：
  2. OR（論理和）：排他的論理和に対して包含的論理和（inclusive OR）
    ゲート： 真理値表
    $\ A\ $$\ B\ $$\ Z\ $
    000
    011
    101
    111
    論理式： $Z=A+B$
    多入力になると、$Z=A+B+C+D+\cdots$　（何れかが$1$の時$1$）
    $Z=\overline{\overline{A}\ \overline{B}\ \overline{C}\ \overline{D}\cdots}$　ととらえると（全てが$0$の時のみ$0$）
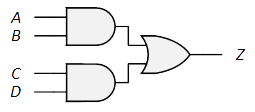
    等価回路：
  3. NOT（論理否定）：インバータ（inverter）とも呼ばれる
    ゲート： 真理値表
    $\ A\ $$\ Z\ $
    01
    10
    論理式： $Z=\overline{A}$
    等価回路：
    NANDやNORの頭の$\circ$は、NOT（インバータ）がくっ付いていると思えば良い！
    NOT（インバータ）のカスケード（直列）接続は、論理的には何も無いのと同じ！
    $Z=\overline{\overline{A}}=A$
  4. NAND（NOT of AND）：論理積の否定
    ゲート： 真理値表
    $\ A\ $$\ B\ $$\ Z\ $
    001
    011
    101
    110
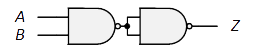
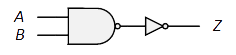
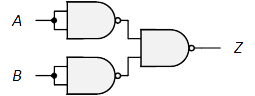
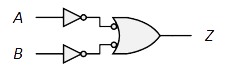
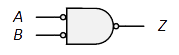
    論理式： $Z=\overline{AB}=\overline{A}+\overline{B}$
    多入力になると、$Z=\overline{ABCD\cdots}$　（全てが$1$の時のみ$0$）
    $Z=\overline{A}+\overline{B}+\overline{C}+\overline{D}+\cdots$
    等価回路：
  5. NOR（NOT of OR）：論理和の否定
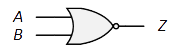
    ゲート： 真理値表
    $\ A\ $$\ B\ $$\ Z\ $
    001
    010
    100
    110
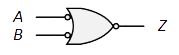
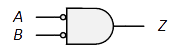
    論理式： $Z=\overline{A+B}=\overline{A}\ \overline{B}$
    多入力になると、$Z=\overline{A+B+C+D+\cdots}$　（何れかが$1$の時$0$）
    $Z=\overline{A}\ \overline{B}\ \overline{C}\ \overline{D}\cdots$　ととらえると（全てが$0$の時のみ$1$）
    等価回路：
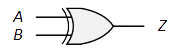
  6. XOR（eXclusive OR：排他的論理和）：EORとも呼ぶ、不一致論理（A≠B）とも言える
    ゲート： 真理値表
    $\ A\ $$\ B\ $$\ Z\ $
    000
    011
    101
    110
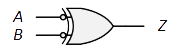
    論理式： $Z=\overline{A}B+A\overline{B}=A\oplus B$
    $Z=\overline{A}\oplus\overline{B}=\overline{\overline{A}}\ \overline{B}+\overline{A}\ \overline{\overline{B}}=A\overline{B}+\overline{A}B$
    等価回路：
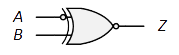
    $Z=\overline{\overline{A}\oplus B}=\overline{\overline{\overline{A}}\ B+\overline{A}\ \overline{B}}=\overline{AB+\overline{A}\ \overline{B}}$
    等価回路：
  7. XNOR（排他的論理和の否定）：一致論理（A＝B）とも言える
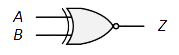
    ゲート： 真理値表
    $\ A\ $$\ B\ $$\ Z\ $
    001
    010
    100
    111
    論理式： $Z=\overline{A}\ \overline{B}+AB=\overline{A\oplus B}$
    $Z=\overline{\overline A\oplus\overline B}=\overline{\overline{\overline{A}}\ \overline{B}+\overline{A}\ \overline{\overline{B}}}=\overline{A\overline{B}+\overline{A}B}$
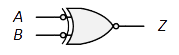
    等価回路：
    $Z=\overline A\oplus B=\overline{\overline{A}}\ B+\overline{A}\ \overline{B}=AB+\overline{A}\ \overline{B}$
    等価回路：

NANDゲートで他の論理を実現する

  1. NOT（論理否定）
    $\overline{AB}=\overline{A}\quad(\because B=A)$
    ＝
  2. AND（論理積）
    $Z=\overline{\overline{AB}}=AB$
    ＝
    ↓
  3. OR（論理和）
    $Z=\overline{\overline{A}\ \overline{B}}=\overline{\overline{A}}+\overline{\overline{B}}=A+B$
    ＝
    ↓

　問題

完備性（completeness）について

　全ての論理関数を表すことができる少数の基本論理関数の集合を完備集合（Complete Set）と呼ぶ。

　完備集合の例

戻る