|
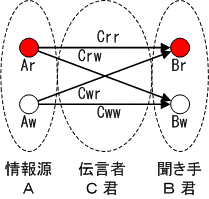
|
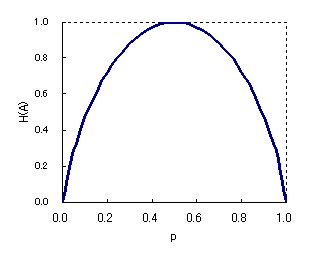
Aのエントロピー H(A) は、
| H(A) = Ar log2 | 1 Ar |
+ Aw log2 | 1 Aw |
(bit) |
| H(A) = H(p) = p log2 | 1 p |
+ (1-p) log2 | 1 1-p |
(bit) |
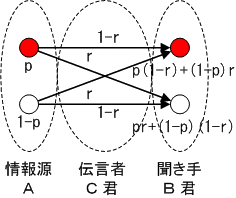
B君が1回の伝言で受け取る平均情報量 H(B) は、
- 対称チャンネル
今、簡単の為に、赤を白と誤る確率と白を赤と誤る確率が同じであるとして、Crw = Cwr = r とします。 Crr = Cww = 1 - r となります。 このような伝言者を対称チャンネルと呼びます。 - Br = ArCrr + AwCwr = p(1-r) + (1-p)r
- Bw = ArCrw + AwCww = pr + (1-p)(1-r)
H(B) = H(p,r) = (p(1-r) + (1-p)r) log2 1 
p(1-r) + (1-p)r+ (pr + (1-p)(1-r)) log2 1 
pr + (1-p)(1-r)(bit) 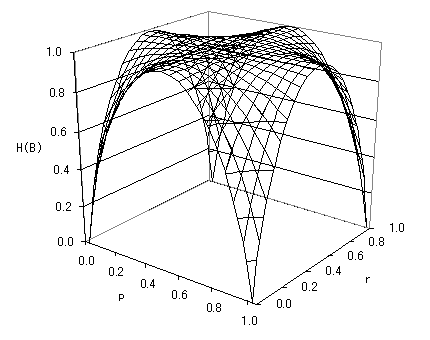
| H(B) = Br log2 | 1 Br |
+ Bw log2 | 1 Bw |
(bit) |
実際の赤白が分かった時点での、B君が受け取る平均情報量 H(B|A) は、C君が新たに作り出したあいまいさを表しており、
- C君が正確に情報を伝える時(Crr = Cww = 1、Crw = Cwr = 0)は、
-
H(B|A) = 0 (bit)
- C君が全くいい加減に伝える時(Crr = Cww = Crw = Cwr = 1/2)は、
-
H(B|A) = 1 (bit)
- C君が対称チャンネルの時(Crw = Cwr = r, Crr = Cww = 1 - r)は、
H(B|A) = H(r) = (1-r) log2 1 
1-r+ r log2 1 
r(bit) 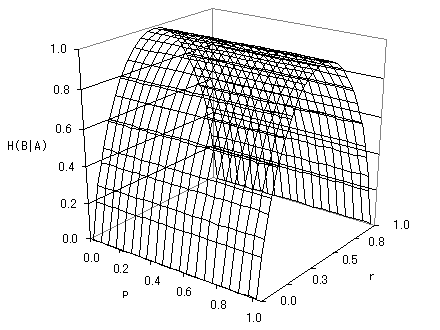
| H(B|A) = | Ar(Crr log2 | 1 Crr |
+ Crw log2 | 1 Crw |
) + | Aw(Cwr log2 | 1 Cwr |
+ Cww log2 | 1 Cww |
) |
伝言結果が分かった時点での、情報源Aに残されるあいまいさ H(A|B) は、
- Ar = 1(Aw = 0)や Ar = 0(Aw = 1)の時、
-
H(A|B) = 0 (bit)
- C君が対称チャンネルの時(Crw = Cwr = r, Crr = Cww = 1 - r)は、
H(A|B) = p((1-r) log2 p(1-r) + (1-p)r 
p(1-r)+ r log2 pr + (1-p)(1-r) 
pr) + (1-p)(r log2 p(1-r) + (1-p)r 
(1-p)r+ (1-r) log2 pr + (1-p)(1-r) 
(1-p)(1-r)) 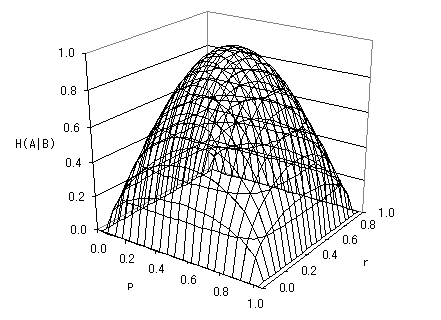
| H(A|B) = | Br(Drr log2 | 1 Drr |
+ Drw log2 | 1 Drw |
) + | Bw(Dwr log2 | 1 Dwr |
+ Dww log2 | 1 Dww |
) |
-
ベイズ則によって、
| P(r,r) = Ar Crr = Br Drr より、 | Drr = | Ar Crr Br |
| P(r,w) = Ar Crw = Bw Dwr より、 | Dwr = | Ar Crw Bw |
| P(w,r) = Aw Cwr = Br Drw より、 | Drw = | Aw Cwr Br |
| P(w,w) = Aw Cww = Bw Dww より、 | Dww = | Aw Cww Bw |
| H(A|B) = | Br( | Ar Crr Br | log2 | Br Ar Crr |
+ | Aw Cwr Br | log2 | Br Aw Cwr |
) |
| + | Bw( | Ar Crw Bw | log2 | Bw Ar Crw |
+ | Aw Cww Bw | log2 | Bw Aw Cww |
) |
| = | Ar(Crr log2 | Br Ar Crr |
+ | Crw log2 | Bw Ar Crw |
) |
| + | Aw(Cwr log2 | Br Aw Cwr |
+ | Cww log2 | Bw Aw Cww |
) |
実際の赤白と、伝言結果の両方を同時に知らされた時のエントロピー、AとBの結合エントロピー H(A, B) は、
- C君が対称チャンネルの時(Crw = Cwr = r, Crr = Cww = 1 - r)は、
H(A, B) = p((1-r) log2 1 
p(1-r)+ r log2 1 
pr) + (1-p)(r log2 1 
(1-p)r+ (1-r) log2 1 
(1-p)(1-r)) 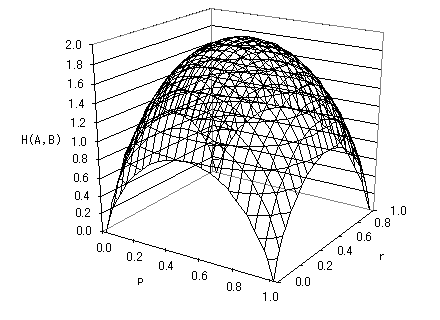
| H(A, B) = | Ar(Crr log2 | 1 Ar Crr |
+ | Crw log2 | 1 Ar Crw |
) |
| + | Aw(Cwr log2 | 1 Aw Cwr |
+ | Cww log2 | 1 Aw Cww |
) |
伝言を得ることで減少した情報源Aのエントロピーは、伝言によって伝えられた情報源Aに関する情報量と考えることができる。 I(B;A) = H(A) - H(A|B) を相互情報量と呼ぶ。
また、Bの得た情報量から、Cが新たに作り出したあいまいさを差し引いたものも、伝言によって伝えられた情報源Aに関する情報量と考えることができる。 I(B;A) = H(B) - H(B|A)
- C君が対称チャンネルの時(Crw = Cwr = r, Crr = Cww = 1 - r)
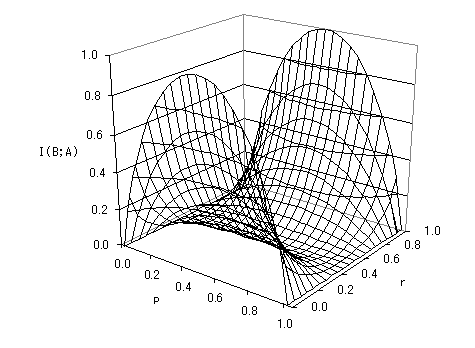
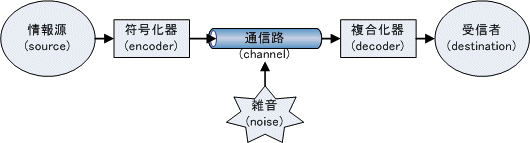
情報源Aを送信信号、伝言者Cを通信路、聞き手Bを受信信号と見ると、通信のモデルとなっており、 相互情報量は受信信号にどれだけ送信情報が含まれるかという尺度になっている。