| オートマトン(Automaton) | オートマトンの構造 | |
| 有限オートマトン (Finite Automaton) | FA | 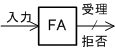 |
| プッシュダウンオートマトン (Push Down Automaton) | FA+スタック | 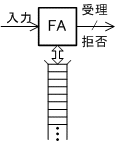 |
| 線形有界オートマトン (Linear Bounded Automaton) | FA+入力と同じ長さのテープ | 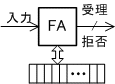 |
| チューリングマシン (Turing Machine) | FA+テープ | 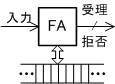 |
もとになる記号の集合(アルファベット)と,生成規則(文法)から,生成することの出来る文字列(言葉)の集合を形式言語(formal language)と呼ぶ。 プログラミング言語などをモデル化したもの。 〜人工言語⇔自然言語
| 文法(Grammer) | 言語(Language) | 受理するオートマトン(Automaton) |
| 正規文法 (Regular Grammer) | 正規言語(3型) | 有限オートマトン (Finite Automaton) |
| 文脈自由文法 (Context Free Grammer) | 文脈自由言語(2型) | プッシュダウンオートマトン (Push Down Automaton) |
| 文脈依存文法 (Context Sensitive Grammer) | 文脈依存言語(1型) | 線形有界オートマトン (Linear Bounded Automaton) |
| 無制約文法(句構造文法) | 句構造言語(0型) | チューリングマシン (Turing Machine) |
形式言語に関してはこちら
オートマトンAの入力記号で作られる入力系列w を、その初期状態から加えたとき、 Aが最終状態になるならば、オートマトンAは入力系列w を受理する(accept)という。 そうでないときには、Aはw を受理しない・拒否する(reject)という。 系列の集合Lが与えられたとき、オートマトンAがその集合に属する系列を全て受理し、それ以外のものを受理しないとき、Aは集合Lを受理するという。
| オートマトン(Automaton) | オートマトンの構造 | |
| 有限オートマトン (Finite Automaton) | FA |  |
| プッシュダウンオートマトン (Push Down Automaton) | FA+スタック |  |
| 線形有界オートマトン (Linear Bounded Automaton) | FA+入力と同じ長さのテープ |  |
| チューリングマシン (Turing Machine) | FA+テープ |  |
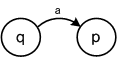
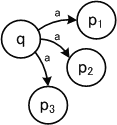
定理:LをNFAで受理される集合とする。このとき、Lを受理するDFAが存在する。
定理:Lがε動作を含むNFAで受理されるならば、Lはε動作を含まないNFAでも受理することができる。
定理:与えられた正規表現 r に対して、L(r) を受理するε動作を含むNFAが存在する。
r = ε |
r = φ |
r = a |
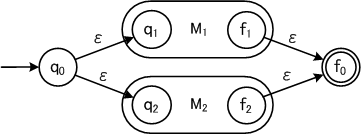

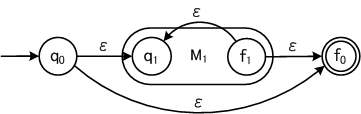
定理:LがDFAで受理されるならば、Lは正規表現で表される。 (これも帰納法で証明することができる。)