グラフ(graph)
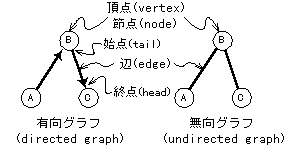
- グラフ(graph)G = (V, E ) は、
頂点(vertex)の空でない有限集合V と辺(edge)の集合E からなる。
- 頂点は点、節点(node)とも呼ばれる、
辺は枝(branch, arc)とも呼ばれる。
- 辺が頂点の順序対 (v, w ) で与えられる場合、
そのグラフを有向(directed)グラフという。
- v は辺 (v, w ) の始点(tail)、w は辺の終点(head)と呼ばれる。
- 辺が相異なる頂点の非順序対 (v, w ) で与えられる場合、
そのグラフを無向(undirected)グラフという。
- (v, w ) ∈ E のとき、
頂点 w は頂点 v に隣接(adjacent)するという。
また、(v, w ) を v から w への辺ともいう。
- v に隣接する頂点の個数を v の出次数(out degree)、
w が隣接する頂点の個数を w の入次数(in degree)という。
- 無向グラフの場合の頂点の次数(degree)は、それに隣接する頂点の個数である。
- 有向道(directed path)とは、(v1, v2), (v2, v3),..., (vn-1, vn) という辺の列である。
これを v1 から vn への有向道といい、その長さは n-1 である。
- v から w への有向道が存在するとき、 w は v から到達可能(reachable)であるという。
- 全ての頂点がある頂点 r から到達可能であるとき、この r を根(root)という。
- 道はその辺が全て異なるとき単純(simple)であるという。
- 道はその頂点が全て異なるとき初等的(elementary)であるという。
但し最初と最後の頂点は一致しても良い。
- 閉路(circuit, loop, closed path)とは、同じ頂点で始まりかつ終わる、長さ1以上の道のことである。
- 有向閉路、サイクル(cycle)とは、同じ頂点で始まりかつ終わる、長さ1以上の有向道のことである。
グラフの表現方法
隣接行列(adjacency matrix)
隣接点リスト(adjacency list)
- 有向木(directed tree)とは、閉路のない有向グラフ(directed acyclic graph)で、以下の条件を満たす:
- 根(root)と呼ばれる、入次数(in deegree)がゼロの頂点が存在する
- 根以外の頂点の入次数(in degree)は1である
- 各頂点には、根からそれに至る有向道が存在する
- 根付木(rooted tree)とも呼ばれる。
- F = (V, E ) を木とする。(v, w ) ∈ E のとき、
v は w の親(father)といい、
w は v の子(son)といわれる。
- v から w への有向道が存在するとき、
v は w の先祖(ancester)といい、
w は v の子孫(descendant)といわれる。
- 子を持たない頂点は、葉(leaf)と呼ばれる。
- 頂点 v とその子孫全体は F の部分木(subtree)といわれる。
頂点 v はその部分木の根である。
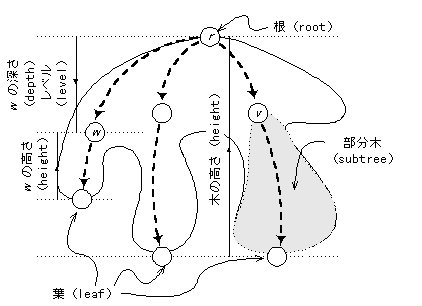
- 木の頂点 v の深さ(depth)、レベル(level)とは、根から v への有向道の長さである。
- 木の頂点 v の高さ(height)とは、v から最も遠い葉への有向道の長さである。
- 木の高さ(height)とは、その根の高さである。
- 順序木(ordered tree)とは、各頂点の子の間に順序が付いている木のことである。
- 順序木を描くときは、各頂点の子は左から右へ順番に書くものとする。
- 2分木(binary tree)とは、以下のような順序木である:
- 各頂点の子は左の子(left son)または右の子(right son)として区別されている
- どの頂点の左の子も右の子も高々1個である
- 根が頂点 v の左の子である部分木 Tl を v の左部分木(left subtree)、
同様に、その根が頂点 v の右の子である部分木 Tr を v の右部分木(right subtree)という。
- 以下のような2分木を完全(complete)2分木という:
ある整数 k が存在して、
- 深さ k 未満の頂点が全て左右の子を持つ
- 深さ k の頂点が全て葉である
- 高さ k の完全2分木は 2k+1-1 個の頂点を持つ
木の走査(traverse)
木 T の根 r が子 v1, v2,..., vk(k > 0)を持っているとする。
k = 0 のとき、T は1個頂点 r だけからなる木とする。
先行順走査(preorder traverse)
- 行きがけ順とも呼ばれる。
- T の先行順走査(preorder traverse)は以下の様に帰納的に定義される:
- 根 r を訪問(走査)する
- 根 v1, v2,..., vk を持つ部分木をこの順に先行順で訪問する。
後行順走査(postorder traverse)
- 帰りがけ順とも呼ばれる。
- T の後行順走査(postorder traverse)は以下の様に帰納的に定義される:
- 根 v1, v2,..., vk を持つ部分木をこの順に後行順で訪問する。
- 根 r を訪問する
- 中がけ順とも呼ばれる。
- 2分木 T に対する中間順走査(inorder traverse)は以下の様に帰納的に定義される:
- 根 r の左部分木を(もし在れば)中間順で訪問する。
- 根 r を訪問する
- 根 r の右部分木を(もし在れば)中間順で訪問する。
- 無向木(undirected tree)とは、閉路のない無向グラフで、連結(connected:任意の2頂点間に道がある)なものをいう。
- 根付き(rooted)無向木とは、特定の頂点が根として指定されている無向木をいう。
- 有向木の全ての辺の向きを無くすと無向木になる
- 根付き無向木に対しても、有向木と同様な述語を用いる
- 違いは:
| 有向木 | 全ての有向道が先祖から子孫へ行く |
| 無向木 | 両方向の道が存在する |
- ラベル付きグラフ(labeled graph)とは、各頂点 v にラベルが与えられているグラフである。
- 重み付きグラフ(weighted graph)とは、各辺 k = (u, v ) に重み w (k ) = w (u, v ) が与えられているグラフである。


